

分析 (1)常数项是不含字母的项,多项式的次数是多项式中次数最高的项的次数;
(2)数轴上两点间的距离就是右边的点对应的数字减去左边的点所对应的数字;
(3)根据点B到原点的距离是点A到原点的距离的两倍列出方程,求出点B的速度.
解答 解: (1)∵不含字母的项是-4,1+2=3,
(1)∵不含字母的项是-4,1+2=3,
所以多项式x3-3xy2-4的常数项-4,次数是3.
即:a=-4,b=3,
答案:-4,3.点A、B在数轴上表示若右图所示.
(2)解:①当点C在点A的左侧,对应的数字为m,
由于AC+BC=11,即(-4-m)+(3-m)=11,
解得m=-6;
②当点C在点B的右侧,对应的数字为n,
由于AC+BC=11,即(n+4)+(n-3)=11,
解得n=5;
所以点C在数轴上所对应的数为5或-6
(3)解:设点B移动的速度为x,则点A移动的速度为2x,
①当移动后点A在原点右侧时,由题意得3+3x=2(2x×3-4),解得x=$\frac{11}{9}$,
②当移动后点A在原点左侧时,由题意3+3x=2(4-2x×3),解得x=$\frac{1}{3}$
∴点B的速度为$\frac{11}{9}$或$\frac{1}{3}$.
答:点B的速度为B的速度为$\frac{11}{9}$或$\frac{1}{3}$
点评 本题是道综合性较强的题目,考查了多项式的次数和常数项,考查了数轴上两点间的距离,考查了列一元一次方程和解一元一次方程.解本题容易只注意点C、A在原点一侧,从而出现漏解的问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
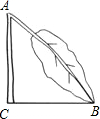 一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)
一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com