

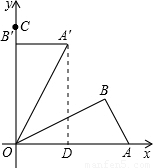
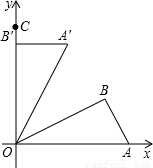
 解:(1)过点A′作A′D垂直于x轴,垂足为D,则四边形OB′A′D为矩形.
解:(1)过点A′作A′D垂直于x轴,垂足为D,则四边形OB′A′D为矩形.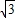 ,
,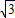 );
);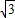 ),在抛物线y=ax2+bx+4上,
),在抛物线y=ax2+bx+4上,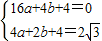 ,
,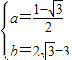 ,
, +(2
+(2 -3)x+4;
-3)x+4;

科目:初中数学 来源:2010年山东省泰安市初中学业考试数学样卷(解析版) 题型:解答题
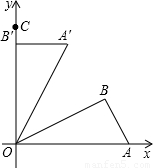
查看答案和解析>>
科目:初中数学 来源:2007年山东省泰安市中考数学试卷(课标卷)(解析版) 题型:解答题
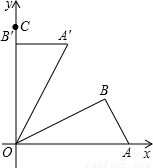
查看答案和解析>>
科目:初中数学 来源:2007年山东省泰安市中考数学试卷(大纲卷)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年山东省泰安市中考数学试卷(大纲卷)(解析版) 题型:选择题
 CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确的个数为( )
CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确的个数为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com