Question

在Rt△ABC中，CD是斜边AB上的高，那么下列锐角三角比中与的值不相等的是

1. A.
   sinA
2. B.
   cosA
3. C.
   cosB
4. D.
   sin∠BCD

Answer 1

B
分析：在△ACD中，根据正弦函数的定义得出sinA=；根据余弦函数的定义得出cosA=；由∠A与∠B互余，得出sinA=cosB=；由同角的余角相等得出∠A=∠BCD，则sinA=sin∠BCD=．
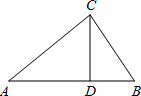
解答：解：如图，∵在Rt△ABC中，CD是斜边AB上的高，
∴∠ACB=90°，∠ADC=∠BDC=90°．
在△ACD中，∵∠ADC=90°，
∴sinA=；cosA=；
∵∠A+∠B=90°，
∴sinA=cosB=；
∵∠A=∠BCD=90°-∠ACD，
∴sinA=sin∠BCD=；
故选B．
点评：本题考查了锐角三角函数的定义，互余两角的三角函数之间的关系，余角的性质，比较简单．