
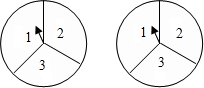
 如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出.现转动两个转盘,等转盘停止转动时,指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小.有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由.
如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出.现转动两个转盘,等转盘停止转动时,指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小.有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由. 科目:初中数学 来源: 题型:
如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出。现转动两个转盘,等转盘停止转动时,指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年湖南省长沙市长铁一中初一上学期末数学卷 题型:解答题
如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出。现转动两个转盘,等转盘停止转动时, 指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。
指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011年湖南省长沙市初一上学期末数学卷 题型:解答题
如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出。现转动两个转盘,等转盘停止转动时,指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com