(1)解:(2ab
2-b
3)
2÷2b
3=(4a
2b
4-4ab
5+b
6)÷2b
3=
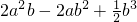
;
(2)解:3x
3-12xy
2=3x(x
2-4y
2)
=3x(x+2y)(x-2y);
(3)解:(2a+b)(b-2a)-b(5b-8a)
=b
2-4a
2-5b
2+8ab
=-4a
2-4b
2+8ab
=-4(a
2-2ab+b
2)
=-4(a-b)
2;
(4)解:(4x-3y)
2-(5x+y)
2-(3x+2y)(4y-3x)
=16x
2-24xy+9y
2-(25x
2+10xy+y
2)-(6xy-9x
2+8y
2)
=16x
2-24xy+9y
2-25x
2-10xy-y
2-6xy+9x
2-8y
2=-40xy,
当

,y=6时,原式=
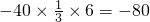
;
(5)解:∵(a-b)
2=a
2+b
2-2ab,
将a-b=1,a
2+b
2=7代入上式,
∴1=7-2ab,
∴ab=3.
分析:(1)先运用完全平方公式计算,再算多项式与单项式的除法;
(2)首先提取公因式3x,再利用平方差公式进行因式分解即可得出答案;
(3)首先利用整式乘法运算去括号,整理再提取公因式进而利用完全平方公式求出即可;
(4)利用完全平方公式以及多项式乘以多项式首先去括号,再利用整式加减运算法则求出即可;
(5)利用完全平方公式(a-b)
2=a
2+b
2-2ab,将已知条件代入即可求出.
点评:此题主要考查了整式的混合运算以及因式分解等知识,因式分解时特别注意如果有公因式首先提取公因式再运用公式进行因式分解,分解因式要彻底,整式的混合运算要牢记公式,运用公式计算比较简便.

 ,y=6
,y=6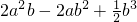 ;
; ,y=6时,原式=
,y=6时,原式=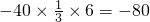 ;
;

 口算题天天练系列答案
口算题天天练系列答案