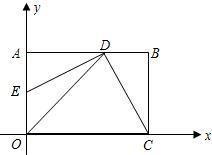
��1������֪����C��3��0����D��2��2����
�ߡ�ADE=90��-��CDB=��BCD��
��AD=BC��AD=2��
��E��0��1������1�֣�
�����E��D��C�������ߵĽ���ʽΪy=ax
2+bx+c��a��0����
����E��������룬��c=1����c=1�͵�D��C������ֱ���룬
��
��2�֣�
����������飬��
�������ߵĽ���ʽΪy=-
x
2+
x+1����3�֣�
��2��EF=2GO��������4�֣�
�ߵ�M�ڸ��������ϣ������ĺ�����Ϊ
��
���M��������Ϊ
����5�֣�
��DM�Ľ���ʽΪy=kx+b
1��k��0��������D��M������ֱ���룬
��
��
���

��DM�Ľ���ʽΪy=-
x+3����6�֣�
��F��0��3����EF=2����7�֣�
����D��DK��OC�ڵ�K����DA=DK��
�ߡ�ADK=��FDG=90�㣬
���FDA=��GDK��
�֡ߡ�FAD=��GKD=90�㣬
���DAF�ա�DKG��
��KG=AF=1��
��OC=3��
��GO=1����8�֣�
��EF=2GO��
��3���ߵ�P��AB�ϣ�G��1��0����C��3��0����
����P��t��2����
��PG
2=��t-1��
2+2
2��PC
2=��3-t��
2+2
2��GC=2��
��PG=PC����t-1��
2+2
2=��3-t��
2+2
2��
���t=2��
��P��2��2������ʱ��Q���P�غϣ�
��Q��2��2������9�֣�
����PG=GC����t-1��
2+2
2=2
2��
���t=1��
��P��1��2����
��ʱGP��x�ᣮGP����������ڵ�һ�����ڵĽ���Q�ĺ�����Ϊ1��
���Q��������Ϊ
��
��Q��1��
������10�֣�
����PC=GC����3-t��
2+2
2=2
2�����t=3��
��P��3��2������ʱPC=GC=2����PCG�ǵ���ֱ�������Σ�
����Q��QH��x���ڵ�H����QH=GH����QH=h��
��Q��h+1��h����
��
-��h+1��
2+
��h+1��+1=h��
���h
1=
��h
2=-2����ȥ����
��Q��
��
������12�֣�
���������������������������ĵ�Q����Q��2��2����Q��1��
����Q��
��
����







 ���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮
���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮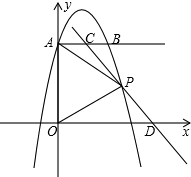 P�ǵ�һ������������һ����PA=PO������P��ֱ�߷ֱ�����AB��x��������C��D����AC=m��OD=n��
P�ǵ�һ������������һ����PA=PO������P��ֱ�߷ֱ�����AB��x��������C��D����AC=m��OD=n�� λ��ƽ�ƺ������ߵĶ����������A��ֱ��x=3��ƽ�ƺ���������ཻ��B����ֱ��OA�ཻ��C��
λ��ƽ�ƺ������ߵĶ����������A��ֱ��x=3��ƽ�ƺ���������ཻ��B����ֱ��OA�ཻ��C��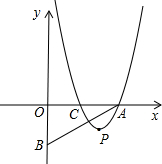
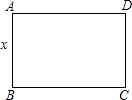 ��AB�ij�Ϊx����λ���ף�������ABCD�����ΪS����λ��ƽ���ף���
��AB�ij�Ϊx����λ���ף�������ABCD�����ΪS����λ��ƽ���ף���