练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．在同一平面内，有4条直线，每两条直线都相交，则交点个数为1或4或7．

    分析 分情况作出图形，根据图形可得交点个数．

    解答 解：如图所示：

    故交点个数为1或4或7．
    故答案为：1或4或7．

    点评 考查了直线、射线、线段，解答此题的关键是找出规律，注意分类思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图1，已知A、B、C三个点．

    （1）分别根据下列要求画图：
    ①画线段AC、直线BC；
    ②过点A画BC的垂线段AD，垂足为D；
    （2）如图2．若三个小区分别住着某公司的员工，B区有30人，D区有15人，C区有10人，且BD=100米，CD=200米，因三个小区在同一直线上，该公司的接送车打算在此间只设一个停靠站，为使所有员工步行到停靠站的路程之和最小，停靠站的位置应设在B．
    A．B区     B．D区    C．C区     D．B、D两区之间．

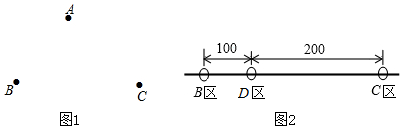
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

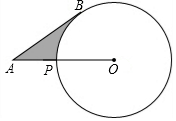    11．如图，已知A为⊙O外一点，连结OA交⊙O于P，AB为⊙O的切线，B为切点，AP=5cm，AB=5$\sqrt{3}$cm，则劣弧$\widehat{BP}$与AB，AP所围成的阴影的面积是（$\frac{25}{2}\sqrt{3}-\frac{25π}{6}$）cm2 

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列各式成立的是（　　）
    A．（a+b）2=a2+b2B．（a-b）2=a2-b2
    C．-x2+4xy-4xy2=-（x-2y）2D．a2+ab+b2=（a+b）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，网格中每个小正方形的边长均为1，等腰直角三角形△ABC、△ADE的顶点都在格点上，点F，G分别为线段DE、BC上的动点，且DF=BG．
    （1）∠C=45°；
    （2）如图1，当DF=$\sqrt{2}$时，求AF+AG的值；
    （3）当AF+AG取得最小值时，请在如图2所示的网格中，用无刻度的直尺，画出线段AF和AG，并简要说明点F和点G的位置是如何找到的（不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．在同一时刻，测得一根高为1.2m的木棍的影长2m，一根旗杆的影长为25m，那么这根旗杆的高度的高度为15m．

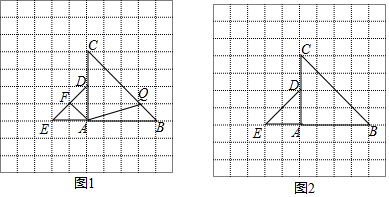
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

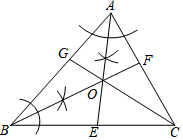    12．如图，AE与BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法不正确的是（　　）
    A．AE、BF是△ABC的内角平分线B．CG也是△ABC的一条内角平分线
    C．AO=BO=COD．点O到△ABC三边的距离相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

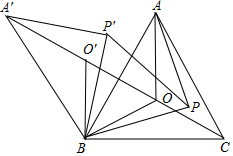    9．如图，O是锐角三角形ABC内一点，∠AOB=∠BOC=∠COA=120°，P是△ABC内不同于O的另一点；△A′BO′、△A′BP′分别由△AOB、△APB逆时针旋转而得，旋转角都为60°，则下列结论：
    ①A′O′+O′O=AO+BO．
    ②A′、O′、O、C在一条直线上．
    ③A′P′+P′P=PA+PB．
    ④PA+PB+PC＞AO+BO+CO．
    其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．先化简，$\frac{x-3}{{x}^{2}-1}$÷$\frac{x-3}{{x}^{2}+2x+1}$-（$\frac{1}{x-1}$+1），然后给x选择一个你喜欢的数代入求值．

    查看答案和解析>>

    同步练习册答案