
 如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:
如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图作,PM⊥BC于M,PN⊥BA于N.利用角平分线的判定定理和性质定理可得PB是∠ABC的平分线,由△PAN≌△PAH,△PCM≌△PCH,推出∠APN=∠APH,∠CPM=∠CPH,由∠MPN=180°-∠ABC=120°,推出∠APC=$\frac{1}{2}$∠MPN=60°,由∠BPN=∠CPA=60°,推出∠CPB=∠APN=∠APH即可一一判断.
解答 解:如图作,PM⊥BC于M,PN⊥BA于N.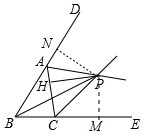
∵∠PAH=∠PAN,PN⊥AD,PH⊥AC,
∴PN=PH,同理PM=PH,
∴PN=PM,
∴PB平分∠ABC,
∴∠ABP=$\frac{1}{2}$∠ABC=30°,故①正确,
∵在Rt△PAH和Rt△PAN中,
$\left\{\begin{array}{l}{PA=PA}\\{PN=PH}\end{array}\right.$,
∴△PAN≌△PAH,同理可证,△PCM≌△PCH,
∴∠APN=∠APH,∠CPM=∠CPH,
∵∠MPN=180°-∠ABC=120°,
∴∠APC=$\frac{1}{2}$∠MPN=60°,故②正确,
在Rt△PBN中,∵∠PBN=30°,
∴PB=2PN=2PH,故③正确,
∵∠BPN=∠CPA=60°,
∴∠CPB=∠APN=∠APH,故④正确.
点评 本题考查角平分线的判定定理和性质定理.全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识,属于中考常考题型.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
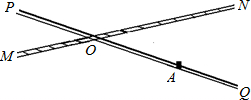 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪音的影响?如果火车行驶的速度为72km/h,居民楼受噪音影响的时间约为多少秒(精确到0.1s)?
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪音的影响?如果火车行驶的速度为72km/h,居民楼受噪音影响的时间约为多少秒(精确到0.1s)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
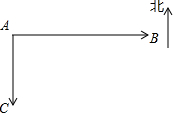 如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.
如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
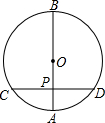 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com