练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
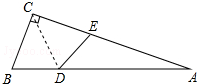
    4．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=24°，则∠BDC等于（　　）
    A．42°B．66°C．69°D．77°

    分析 根据三角形内角和定理求出∠B的度数，根据翻折变换的性质求出∠BCD的度数，根据三角形内角和定理求出∠BDC．

    解答 解：在△ABC中，∠ACB=90°，∠A=24°，
    ∴∠B=90°-∠A=66°．
    由折叠的性质可得：∠BCD=$\frac{1}{2}$∠ACB=45°，
    ∴∠BDC=180°-∠BCD-∠B
    =69°．
    故选：C．

    点评 本题考查的是翻折变换和三角形内角和定理，理解翻折变换的性质、熟记三角形内角和等于180°是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．一元二次方程x2+2x-4=0的根的情况为（　　）
    A．没有实数根B．有两个相等的实数根
    C．有两个不相等的实数根D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程：4x2+5x=81．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．点A（x1，y1）、B（x2，y2）分别在双曲线y=-$\frac{1}{x}$的两支上，若y1+y2＞0，则x1+x2的范围是（　　）
    A．x1+x2＞0B．x1+x2≥0C．x1+x2＜0D．x1+x2＞1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．2015的倒数是（　　）
    A．2015B．$\frac{1}{2015}$C．-2015D．-$\frac{1}{2015}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列四个图形中，不是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

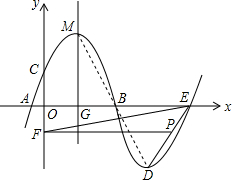    16．如图，抛物线m：y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4与x轴交于点A、B，顶点为M（3，$\frac{25}{4}$），将抛物线m绕点B旋转180°得到新的抛物线n，此时A点旋转至E点，M点旋转至D点．
    （1）求A、B点的坐标；
    （2）求抛物线n的解析式；
    （3）若点P是线段ED上一个动点（E点除外），过点P作y轴的垂线，垂足为F，连接EF．如果P点的坐标为（x，y），△PEF的面积为s，求s与x的函数关系式，写出自变量x的取值范围；如果s有最大值，请求出s的最大值，如果没有请说明理由；
    （4）设抛物线m的对称轴与x轴的交点为G，以G为圆心，A、B两点的距离为直
    径作⊙G，试判断直线CM与⊙G的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

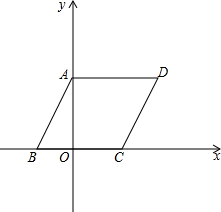    14．如图，?ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．
    （1）写出A、B两点的坐标．
    （2）若点E为x轴正半轴上的点，且S△AOE=$\frac{16}{3}$，求经过D、E两点的直线解析式，并判断△AOE与△DAO是否相似？
    （3）若点M在平面直角坐标系内，则在直线AB上是否存在点F使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出其中两个F点的坐标；若不存在，请说明理由．
    （4）过点O的一条直线OM将平行四边形ABCD的面积分成两个相等的部分，求这条直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．平面直角坐标系中，与点（-2，1）关于原点对称的点的坐标是（　　）
    A．（-2，1）B．（-2，-1）C．（2，-1）D．（2，1）

    查看答案和解析>>

    同步练习册答案