Question

如图，二次函数的图象与x轴交于点A（-3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

（1）请直接写出点D的坐标：
（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；
（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

 

Answer 1

【答案】

（1）（﹣3，4）；（2）P为AO中点时，OE的最大值为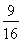；(3)存在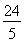，或.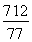

【解析】

试题分析：（1）将点A的坐标代入二次函数的解析式求得其解析式，然后求得点B的坐标即可求得正方形ABCD的边长，从而求得点D的纵坐标；

（2）PA=t，OE=l，利用△DAP∽△POE得到比例式，从而得到有关两个变量的二次函数，求最值即可；

（3）分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积．

试题解析：（1）（﹣3，4）；

（2）设PA=t，OE=l

由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE

∴

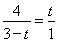
∴l=﹣

∴当t=时，l有最大值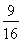

即P为AO中点时，OE的最大值为；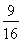

（3）存在．

①点P点在y轴左侧时，P点的坐标为（﹣4，0）

由△PAD∽△OEG得OE=PA=1

∴OP=OA+PA=4

∵△ADG∽△OEG

∴AG：GO=AD：OE=4：1

∴AG=，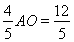

∴重叠部分的面积=；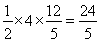

②当P点在y轴右侧时，P点的坐标为（4，0），

此时重叠部分的面积为.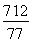

考点: 二次函数综合题．