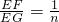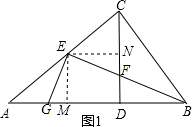
解:(1)证明:如图1,过E作EM⊥AB于M,EN⊥CD于N,
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴AD=CD,
∵点E为AC的中点,CD⊥AB,EN⊥DC,
∴EN=

AD,
∴EM=

CD,
∴EN=EM,
∵∠GEB=90°,∠MEN=90°,
∴∠NEF=∠GEM,
∴
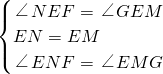
,
∴△EGM≌△EFN,(ASA)
∴EG=EF
(2)
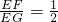
证明如图(2):过点E作EM⊥CD于点M,作EN⊥AB于点N,

∴∠ENA=∠CME=∠EMF=90°.
∵CD⊥AB于点D,
∴∠CDA=90°.
∴EM∥AD.∠A=∠CEM.
∴△EMC∽△ANE.∴
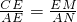
∵EM∥AD,∴∠NEM=90.即∠1+∠2=90°.
∵EG⊥BE,∴∠3+∠2=90°,
∴∠MEF=∠GEN.
∴△EFM∽△EGN.∴
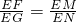
.
∵∠ACB=90°,AC=BC,∴∠A=45°,∴AN=EN.
∴
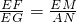
,
∴
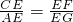
∵
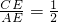
,
∴
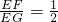
.
(3)∴
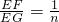
证明如图(3):过点E作EM⊥CD于点M,作EN⊥AB于点N,
∴∠ENA=∠CME=∠EMF=90°.
∵CD⊥AB于点D,
∴∠CDA=90°.
∴EM∥AD.∠A=∠CEM.
∴△EMC∽△ANE.∴
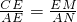
∵EM∥AD,∴∠NEM=90.即∠2+∠3=90°.
∵EG⊥BE,∴∠3+∠2=90°,
∴∠MEF=∠GEN.
∴△EFM∽△EGN.∴
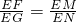
.
∵∠ACB=90°,AC=BC,∴∠A=45°,∴AN=EN.
∴
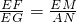
,
∴
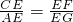
∵
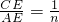
∴
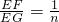
,
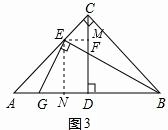
故答案为:(1)EF=EG,(3)
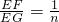
分析:(1)根据全等三角形的证明方法利用ASA得出△EFM≌△EGN,即可得出EF=EG;
(2)根据已知首先求出∠ENG=∠FEM,再得出∠ENG=∠EMF,即可得出△EFM∽△EGN,再利用相似三角形的性质得出答案即可.
点评:本题考查了相似三角形的判定与性质,平行线的性质,等腰直角三角形的性质的运用.

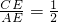 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明; ,线段EF与EG的数量关系是______.
,线段EF与EG的数量关系是______.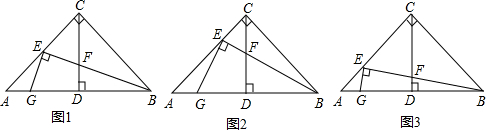
 解:(1)证明:如图1,过E作EM⊥AB于M,EN⊥CD于N,
解:(1)证明:如图1,过E作EM⊥AB于M,EN⊥CD于N, AD,
AD, CD,
CD,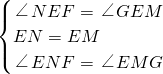 ,
,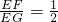

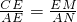
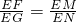 .
.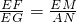 ,
,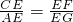
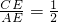 ,
,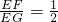 .
.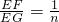
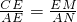
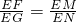 .
.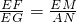 ,
,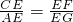
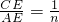
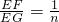 ,
,