
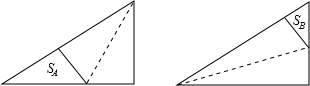
 解:设AC=FH=3x,则BC=GH=4x,AB=GF=5x.
解:设AC=FH=3x,则BC=GH=4x,AB=GF=5x.| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第6期 总第162期 沪科版 题型:022
如图,△
DEF与△PQR相似,记作△DEF________△PQR,读作________,△DEF与△PQR的相似比k1=________,△PQR与△DEF的相似比k2=________.一般k1=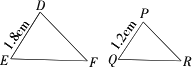
查看答案和解析>>
科目:初中数学 来源:台湾省中考真题 题型:单选题
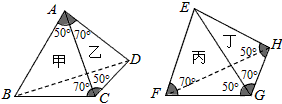
[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com