
分析 (1)根据二次根式的加减可以解答本题;
(2)先化简括号内的式子,然后根据乘法分配律即可解答本题.
解答 解:(1)$\frac{\sqrt{8}}{2}$+(-$\frac{1}{3}$)-1-($\sqrt{10}$-$\sqrt{5}$)0-$\frac{2}{\sqrt{2}}$
=$\frac{2\sqrt{2}}{2}+(-3)-1-\frac{2\sqrt{2}}{2}$
=-4;
(2)($\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2$\sqrt{\frac{1}{x}}$)×$\sqrt{x}$
=$(\frac{2}{3}×3\sqrt{x}+\frac{3\sqrt{x}}{2}-\frac{2\sqrt{x}}{x})×\sqrt{x}$
=2x+$\frac{3x}{2}$-2
=$\frac{7x}{2}-2$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
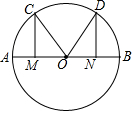 如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.
如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:$\widehat{AC}$=$\widehat{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.
如图,∠BAC=∠BEF=90°,AB=AC=3,EB=EF,BF=1,O为FC的中点,当△EBF绕点B旋转(在△ABC所在平面内)时,AO的最大值为$\frac{3\sqrt{2}+1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
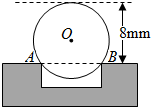 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
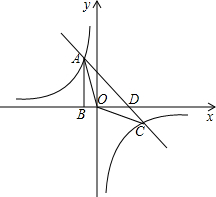 如图,点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$
如图,点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com