
分析 (1)三一分组、二二分组都不行,考虑拆项,把-4y3拆成-y3与x3组成立方差公式,剩余三项组,组后提取公因式;
(2)题目5项,考虑三二组合后再提取公因式.
解答 (1)x3-6x2y+9xy2-4y3
=x3-y3-6x2y+9xy2-3y3
=(x3-y3)-(6x2y-9xy2+3y3)
=(x-y)(x2+xy+y2)-3y(2x-y)(x-y)
=(x-y)(x2+xy+y2-6xy+3y2)
=(x-y)(x2-5xy+4y2)
=(x-y)(x-4y)(x-y)
=(x-y)2(x-4y)
(2)x4+2x3y-3x2y2-4xy3+4y4
=(x4+2x3y-3x2y2)-(4xy3-4y4)
=x2(x2+2xy-3y2)-4y3(x-y)
=x2(x+3y)(x-y)-4y3(x-y)
=(x-y)(x3+3x2y-4y3)
=(x-y)[(x3-y3)+(3x2y-3y3)]
=(x-y)[(x-y)(x2+xy+y2)+3y(x+y)(x-y)]
=(x-y)[(x-y)(x2+xy+y2+3xy+3y2)]
=(x-y)2(x2+4xy+4y2)
=(x-y)2(x+2y)2
点评 本题考查了因式分解的分组分解法,拆项恰当分组是关键.四项一般考虑一三或者二二分组,一三分组后运用平方差,二二分组后考虑提取公因式,五项,一般按按二三分组,分组后提取公因式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
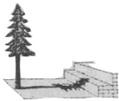 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )| A. | 6.93米 | B. | 8米 | C. | 11.8米 | D. | 12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,若CD=2cm,则AC=2+$2\sqrt{2}$(cm).
如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的角平分线,DE⊥AB,垂足为E,若CD=2cm,则AC=2+$2\sqrt{2}$(cm).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.
如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 1:$\sqrt{6}$ | D. | 4:9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com