
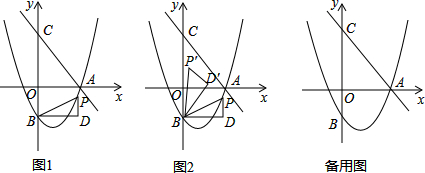
分析 (1)先确定出点A的坐标,再用待定系数法求出抛物线解析式;
(2)由△BDP为等腰直角三角形,判断出BD=PD,建立m的方程计算出m,从而求出PD;
(3)分点P′落在x轴和y轴两种情况计算即可
解答 解:(1)∵点C(0,4)在直线y=-$\frac{4}{3}$x+n上,
∴n=4,
∴y=-$\frac{4}{3}$x+4,
令y=0,
∴x=3,
∴A(3,0),
∵抛物线y=$\frac{2}{3}$x2+bx+c经过点A,交y轴于点B(0,-2).
∴c=-2,6+3b-2=0,
∴b=-$\frac{4}{3}$,
∴抛物线解析式为y=$\frac{2}{3}$x2-$\frac{4}{3}$x-2,
(2)∵点P的横坐标为m,且点P在抛物线上,
∴P(m,$\frac{2}{3}$m2-$\frac{4}{3}$m-2),D(m,-2).
若△BDP为等腰直角三角形,则PD=BD.
①当点P在直线BD上方时,PD=$\frac{2}{3}$m2-$\frac{4}{3}$m.
(ⅰ)若点P在y轴左侧,则m<0,BD=-m.
∴$\frac{2}{3}$m2-$\frac{4}{3}$m=-m,
∴m1=0(舍去),m2=$\frac{1}{2}$(舍去).
(ⅱ)若点P在y轴右侧,则m>0,BD=m.
∴$\frac{2}{3}$m2-$\frac{4}{3}$m=m,
∴m3=0(舍去),m4=$\frac{7}{2}$.
②当点P在直线BD下方时,m>0,BD=m,PD=-$\frac{2}{3}$m2+$\frac{4}{3}$m.
-$\frac{2}{3}$m2+$\frac{4}{3}$m=m,
∴m5=0(舍去),m6=$\frac{1}{2}$.
综上所述,m=$\frac{7}{2}$或m=$\frac{1}{2}$.
即当△BDP为等腰直角三角形时,PD的长为$\frac{7}{2}$或$\frac{1}{2}$.
(3)∵∠PBP'=∠OAC,OA=3,OC=4,
∴AC=5,
∴sin∠PBP'=$\frac{4}{5}$,cos∠PBP'=$\frac{3}{5}$,
①当点P'落在x轴上时,过点D'作D'N⊥x轴,垂足为N,交BD于点M,
∠DBD'=∠ND'P'=∠PBP',
如图1,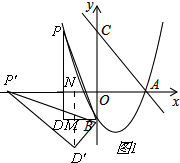
由旋转知,P'D'=PD=$\frac{2}{3}$m2-$\frac{4}{3}$m,
在Rt△P'D'N中,cos∠ND'P'=$\frac{ND′}{P′D′}$=cos∠PBP'=$\frac{3}{5}$,
∴ND'=$\frac{3}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m),
在Rt△BD'M中,BD'=-m,sin∠DBD'=$\frac{D′M}{BD′}$=sin∠PBP'=$\frac{4}{5}$,
∴D'M=-$\frac{4}{5}$m,
∴ND'-MD'=2,
∴$\frac{3}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m)-(-$\frac{4}{5}$m)=2,
∴m=$\sqrt{5}$(舍),或m=-$\sqrt{5}$,
如图2,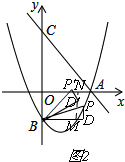
同①的方法得,ND'=$\frac{3}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m),MD'=$\frac{4}{5}$m
∵ND'+MD'=2,
∴$\frac{3}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m)+$\frac{4}{5}$m=2,
∴m=$\sqrt{5}$,或m=-$\sqrt{5}$(舍),
∴P(-$\sqrt{5}$,$\frac{4\sqrt{5}+4}{3}$)或P($\sqrt{5}$,$\frac{-4\sqrt{5}+4}{3}$),
②当点P'落在y轴上时,如图3,
过点D′作D′M⊥x轴,交BD于M,过点P′作P′N⊥y轴,交MD'的延长线于点N,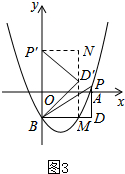
∴∠DBD′=∠ND′P′=∠PBP′,
同①的方法得,P'N=$\frac{4}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m),BM=$\frac{3}{5}$m,
∵P′N=BM,
∴$\frac{4}{5}$($\frac{2}{3}$m2-$\frac{4}{3}$m)=$\frac{3}{5}$m,
∴m=$\frac{25}{8}$,
∴P($\frac{25}{8}$,$\frac{11}{32}$).
∴P(-$\sqrt{5}$,$\frac{4\sqrt{5}+4}{3}$)或P($\sqrt{5}$,$\frac{-4\sqrt{5}+4}{3}$)或P($\frac{25}{8}$,$\frac{11}{32}$).
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,锐角三角函数,等腰直角三角形的性质,解本题的关键是构造直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
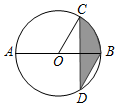 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )| A. | 4π | B. | 2π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com