
 解:如图1,当小丽家在小亮家和小华家之间时,
解:如图1,当小丽家在小亮家和小华家之间时, AD=600米,
AD=600米, AC=
AC= ×600=300米,
×600=300米, AC=200米,
AC=200米, AC=300米,
AC=300米,

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:044
“翔风花园”社区的工作人员想要了解他们所生活的小区里老年人的健康状况,小明、小亮、小华和小丽四位同学进行了社会调查,其调查结果如下:
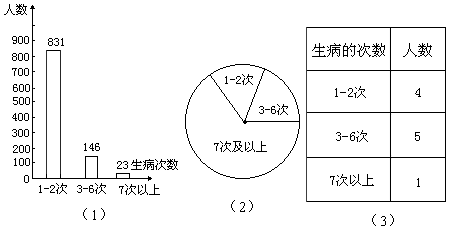
小明在社区附近公园里调查了1000名老年人,他们一年中生病的次为图(1)所示.
小丽在社区医院调查了1000名老年病人,他们一年中生病的次数为图(2)所示.
小亮调查了10名老年邻居,他们一年中生病的次数如图(3)所示.
小华利用派出所的户籍网随机调查了该社区10%的老年人,发现他们一年平均生病3次左右.
(1)你同意他们的做法吗?说说理由,
(2)为了了解你所住社区的老年人的健康状况,你认为应当怎样收集数据?与同伴交流.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省十堰市八年级上学期期末调研考试数学试卷(带解析) 题型:计算题
数学课上,张老师出示了问题:如图1,△ABC是等边三角形,点D是边BC的中点.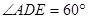 ,且DE交△ABC外角
,且DE交△ABC外角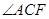 的平分线CE于点E,求证:AD=DE.
的平分线CE于点E,求证:AD=DE.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接MD,则△BMD是等边三角形,易证△AMD≌△DCE,所以AD=DE.在此基础上,同学们作了进一步的研究: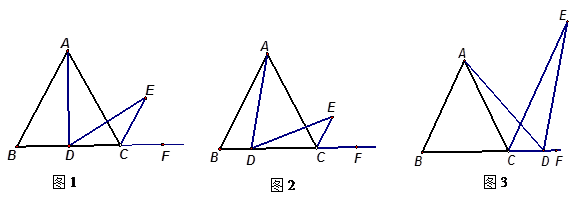
(1)小颖提出:如图2,如果把“点D是边BC的中点”改为“点D是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AD=DE”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小亮提出:如图3,点D是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AD=DE”仍然成立.你认为小华的观点 (填“正确”或“不正确”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com