
 如图所示,在Rt△ABC中,∠A=90°,AB=3cm,AC=4cm.
如图所示,在Rt△ABC中,∠A=90°,AB=3cm,AC=4cm. ;FM=FP-PM=2-
;FM=FP-PM=2- =
= ,
, ,
, FP•PQ=
FP•PQ= •2•
•2• =
= .
. ;同样,NM:AB=FM:CB,得NM=
;同样,NM:AB=FM:CB,得NM= ,
, FN•NM=
FN•NM= •
•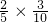 =
= ,
, -
- =
=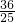 ;
; x,
x, x,∴NC=NM+MC=
x,∴NC=NM+MC= x+
x+ x=
x= x,
x, x,
x, ;对于图2中点P2的位置,容易求得P2C=
;对于图2中点P2的位置,容易求得P2C= .
. 时,
时, PC•MP-
PC•MP- FN•NM
FN•NM x•
x• x-
x-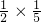 x•
x• x=
x= x2,
x2, <x≤
<x≤ 时,y=S△ABC-S△CPM=6-
时,y=S△ABC-S△CPM=6- •x•
•x• x=6-
x=6- x2;
x2; <x<5时,y=S△MPB=
<x<5时,y=S△MPB= •(5-x)•
•(5-x)• (5-x)=
(5-x)= (3-x)2.
(3-x)2. 时,y=
时,y= x2;
x2; <x≤
<x≤ 时,y=6-
时,y=6- x2;
x2; x<5时,y=
x<5时,y= (3-x)2.
(3-x)2.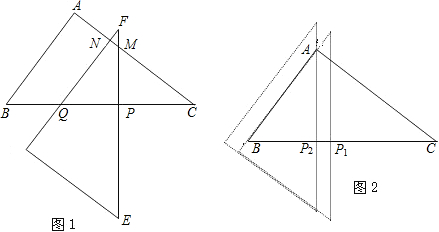
 x,MN=
x,MN= x,所以NC=NM+MC=
x,所以NC=NM+MC= x,从而AN=AC-NC=4-
x,从而AN=AC-NC=4- x,由AN=0求出x=
x,由AN=0求出x= ;对于图2中点P2的位置,容易求得P2C=
;对于图2中点P2的位置,容易求得P2C= ,
, 时,由y=S△FPQ-S△FNM=S△CPM-S△FNM=
时,由y=S△FPQ-S△FNM=S△CPM-S△FNM= PC•MP-
PC•MP- FN•NM可以求出函数解析式;
FN•NM可以求出函数解析式; <x≤
<x≤ 时,由y=S△ABC-S△CPM可以求出函数解析式;
时,由y=S△ABC-S△CPM可以求出函数解析式; <x<5时,由y=S△MPB=
<x<5时,由y=S△MPB= •(5-x)•
•(5-x)• (5-x)求出函数解析式.
(5-x)求出函数解析式.

科目:初中数学 来源: 题型:
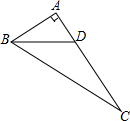 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com