
如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.

△OMN是等腰直角三角形.理由见解析.
【解析】
试题分析:连接OA.先证得△OAN≌△OBM,然后根据全等三角形的对应边相等推知OM=ON;然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°,即△OMN是等腰直角三角形.
试题解析:△OMN是等腰直角三角形.
理由:连接OA.
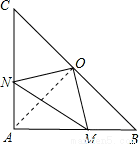
∵在△ABC中,∠A=90°,AB=AC,O是BC的中点,
∴AO=BO=CO(直角三角形斜边上的中线是斜边的一半);
∠B=∠C=45°;
在△OAN和OBM中,

∴△OAN≌△OBM(SAS),
∴ON=OM;
∴∠AON=∠BOM;
又∵∠BOM+∠AOM=90°,
∴∠NOM=∠AON+∠AOM=90°,
∴△OMN是等腰直角三角形.
考点:1.等腰直角三角形;2.全等三角形的判定与性质.


科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片八年级12月月考数学试卷(解析版) 题型:选择题
下列函数关系式:①y=-x;②y=2x+11;③y=x2+x+1 ④y=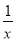 .其中一次函数的个数是
.其中一次函数的个数是
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南京江宁湖熟片七年级上学期期中检测数学试卷(解析版) 题型:选择题
多项式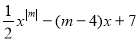 是关于
是关于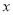 的四次三项式,则
的四次三项式,则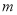 的值是( )
的值是( )
A.4 B.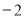 C.
C.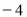 D.
D.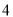 或
或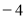
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com