
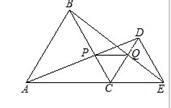
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:①AD=BE ②AP=BQ ③ ∠AOB=60° ④DE=DP  其中正确的结论有
其中正确的结论有
A.① ② ③ B.① ③ ④ C.① ② D. ② ③ ④
A
【解析】∵等边△ABC和等边△CDE,∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴180°-∠ECD=180°-∠ACB,即∠ACD=∠BCE,在△ACD与△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,故①小题正确;
∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°(已证),
∴∠ACQ=180°-60°×2=60°,∠ACB=∠ACQ=60°,
在△ACP与△BCQ中,∠CAD=∠CBE,AC=BC,∠ACB=∠ACQ=,
∴△ACP≌△BCQ(ASA),∴AP=BQ,故②小题正确;
∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠CBE+∠BEC=∠BCA=60°,
∴∠CAD+∠BEC=60°,∴∠AOB=60°,故③小题正确;
∵AD=BE,AP=BQ,∴AD-AP=BE-BQ,即DP=QE,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,∴∠DQE≠∠CDE,故④小题错误.综上所述,正确的是①②③.故选A.


科目:初中数学 来源: 题型:
 24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有
24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有查看答案和解析>>
科目:初中数学 来源: 题型:
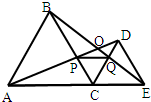 10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:
如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com