
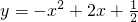 的最大值相同的是
的最大值相同的是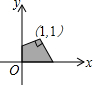
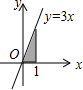
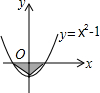
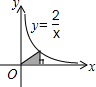
 配成y=-(x-1)2+1,得到y的最大值为
配成y=-(x-1)2+1,得到y的最大值为 ;在选项A中,作AD⊥y轴于D,AE⊥x轴于E,AD=AE=1,可证△ADB≌△AEC,则S阴影部分=S正方形ADOE=1;在B选项中,先确定A点坐标,则可得到S阴影部分=S△OAB=
;在选项A中,作AD⊥y轴于D,AE⊥x轴于E,AD=AE=1,可证△ADB≌△AEC,则S阴影部分=S正方形ADOE=1;在B选项中,先确定A点坐标,则可得到S阴影部分=S△OAB= ×1×3=
×1×3= ;在C选项中,先确定A(0,-1),B(-1,0),C(1,0),则S阴影部分=S△ABC=
;在C选项中,先确定A(0,-1),B(-1,0),C(1,0),则S阴影部分=S△ABC= ×2×1=1;在D选项中,利用k的几何意义得到S阴影部分=S△OAB=
×2×1=1;在D选项中,利用k的几何意义得到S阴影部分=S△OAB= ×2=1.
×2=1. =-(x-1)2+
=-(x-1)2+ ,
, ,
, 如图,作AD⊥y轴于D,AE⊥x轴于E,
如图,作AD⊥y轴于D,AE⊥x轴于E, ×1×3=
×1×3= ,所以B选项正确;
,所以B选项正确; ×2×1=1,所以C选项错误;
×2×1=1,所以C选项错误; ×2=1,所以D选项错误.
×2=1,所以D选项错误. )2+
)2+ ,当a>0,y最小值=
,当a>0,y最小值= ;当a<0,y最,大值=
;当a<0,y最,大值= ;对于一次函数和反比例函数的性质要熟练掌握.
;对于一次函数和反比例函数的性质要熟练掌握. 

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年安徽省淮北市五校九年级(上)第二次联考数学试卷(解析版) 题型:选择题
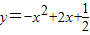 的最大值相同的是( )
的最大值相同的是( )

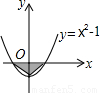
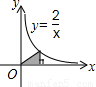
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com