（2013•鹰潭模拟）某校九年级（1）班数学兴趣小组开展了一次活动，过程如下：
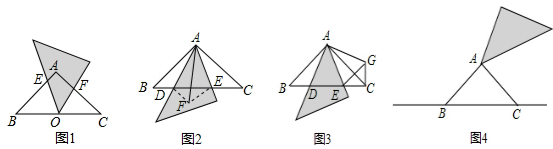
如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小明将一块直角三角板的直角顶点放在斜边BC边的中点O上，从BC边开始绕点A顺时针旋转，其中三角板两条直角边所在的直线分别交AB、AC于点E、F．
（1）小明在旋转中发现：在图1中，线段AE与CF相等．请你证明小明发现的结论；
（2）小明将一块三角板中含45°角的顶点放在点A上，从BC边开始绕点A顺时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．当0°＜α≤45°时，小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系：
BD
2+CE
2=DE
2．同组的小颖和小亮随后想出了两种不同的方法进行解决：
小颖的方法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）；
小亮的方法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）．
请你从中任选一种方法进行证明；
（3）小明继续旋转三角板，在探究中得出：当45°＜α＜135°且α≠90°时，等量关系BD
2+CE
2=DE
2仍然成立．现请你继续探究：当135°＜α＜180°时（如图4），等量关系BD
2+CE
2=DE
2是否仍然成立？若成立，给出证明；若不成立，说明理由．
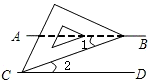小明将等腰直角三角板放在两条平行线上，如图所示．若∠2=20°，则∠1等于
小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长．（两个三角板分别是等腰直角三角形和含30°的直角三角形）
（2012•泉港区质检）小明将等腰直角三角板放在两条平行线上，如图所示．若∠2=20°，则∠1等于（ ）