
 的值为________.
的值为________.
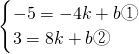 ,
, ,代入②得,b=-
,代入②得,b=- ,
, x-
x- ,
, m-
m- =0,n=-
=0,n=- ,
, ,n=-
,n=- ,
, =
= ×(-
×(- )=-
)=- .
. .
.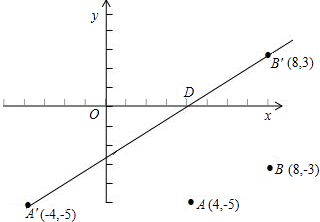


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
 27、如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=
27、如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=查看答案和解析>>
科目:初中数学 来源: 题型:
 在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,….
在直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,….查看答案和解析>>
科目:初中数学 来源: 题型:填空题
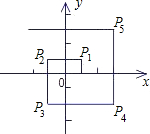 如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=________.
如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com