
分析 (1)根据关于x的一元二次方程x2+(m+3)x+m+1=0的根的判别式△=b2-4ac的符号来判定该方程的根的情况;
(2)根据根与系数的关系求得x1+x2=-(m+3),x1•x2=m+1;然后由已知条件列出关于m的方程,通过解该方程即可求得m的值.
解答 (1)证明:∵△=(m+3)2-4(m+1)
=(m+1)2+4,
∵无论m取何值,(m+1)2+4恒大于0,
∴原方程总有两个不相等的实数根.
(2)解:∵x1,x2是原方程的两根,
∴x1+x2=-(m+3),x1•x2=m+1,
∵x1+x2=x1x2,
∴-(m+3)=m+1,
解得m=-2.
点评 本题考查了根与系数的关系、根的判别式.一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
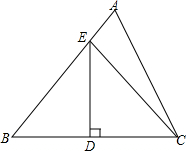 如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )| A. | 18 | B. | 20 | C. | 26 | D. | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)2=4 | B. | -52=25 | C. | $\frac{{4}^{2}}{5}$=$\frac{16}{25}$ | D. | -(-$\frac{1}{9}$)2=-$\frac{1}{81}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com