
分析 根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,结合已知条件,可知x1、x2、x3的最小一组值是2、3、4;根据抛物线,知它与x轴的交点是(0,0)和(-a,0),对称轴是x=-$\frac{a}{2}$.因此要满足已知条件,则其对称轴应小于2.5.
解答 解:∵x1、x2、x3为△ABC的三边,且x1<x2<x3,
∴x1、x2、x3的最小一组值是2、3、4.
∵抛物线y=x2+ax与x轴的交点是(0,0)和(-a,0),对称轴是x=-$\frac{a}{2}$,
∴若对所有的正整数x1、x2、x3都满足y1<y2<y3,则-$\frac{a}{2}$<2.5
解得:a>-5.
故答案为:a>-5.
点评 此题综合考查了三角形的三边关系和抛物线的有关知识,掌握抛物线的对称性是解题的关键.


科目:初中数学 来源: 题型:解答题
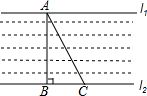 如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
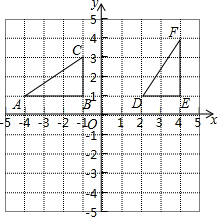 如图,△ABC和△DEF在直角坐标系中的位置如图所示.
如图,△ABC和△DEF在直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
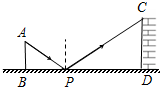 如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )
如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )| A. | 6米 | B. | 8米 | C. | 10米 | D. | 15米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
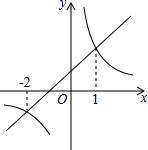 一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.
一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
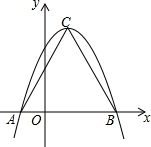 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com