
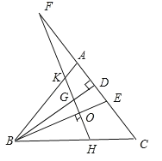
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H .下列结论:
①∠DBE=∠F;②∠F=∠BAC-∠C;
③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
A.1B.2C.3D.4
【答案】C
【解析】
根据BD⊥FD,FH⊥BE和∠FGD=∠BGH,证明结论正确;
②证明∠DBE=∠BAC-∠C,根据①的结论,证明结论正确;
③根据角平分线的定义和三角形外角的性质证明结论正确;
④根据角平分线的定义和三角形外角的性质证明结论正确.
①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
正确;
②
∠ABD=90°∠BAC,
∠DBE=∠ABE∠ABD=∠ABE90°+∠BAC=∠CBD∠DBE90°+∠BAC,
∵∠CBD=90°∠C,
∴∠DBE=∠BAC∠C∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC∠C∠DBE,
②错误;
③∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①③④.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】根据问题进行证明:
(1)已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P,求证:AP=BQ.
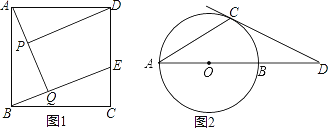
(2)如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D且∠A=∠D.求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)有理数![]() 、
、![]() 、
、![]() 在数轴上的对应点如图所示,化简代数式:
在数轴上的对应点如图所示,化简代数式:![]()
![]()
(2)哈市某垃圾处理场一周处理生活垃圾任务为210吨,计划每天处理30吨,由于各种原因,实际每天处理量与计划相比有出入,某周七天的实际处理情况记录如下:
+6;-3;+4;-1;+2;-5;0
①垃圾场这一周实际处理生活垃圾是多少吨?
②若该垃圾场实行计量工资,每处理一吨生活垃圾给300元,同时又规定超额处理一吨垃圾另外奖100元,完不成任务的少处理一吨另外扣100元,那么该场工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
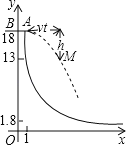
【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=![]() (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com