
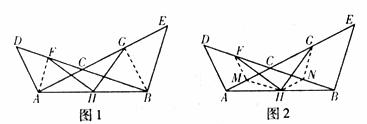
如图,已知AE、BD相交于点C,AC=AD,BC=BE,F、G、H分别是DC、CE、AB的中点。求证:(1)HF=HG;(2)∠FHG=∠DAC

证明:(1)证法一:如图1,连接AF、BG
∵AC=AD,BC=BE,F、G分别是DC、CE的中点,
∴AF⊥BD,BG⊥AE
在直角三角形AFB中,
∵H是斜边AB中点,
∴FH=![]() AB
AB
同理可证HG=![]() AB
AB
∴HF=HG
证法二:如图2,取AC中点M,BC中点N,连接MF、MH、NG、NH,
∵F、G、H分别是CD、CE、AB中点,
∴FM=AD且FM∥AD,NG=![]() BE且NG∥BE,
BE且NG∥BE,
MH=![]() CB且MH∥CB,HN=
CB且MH∥CB,HN=![]() AC且HN∥AC
AC且HN∥AC
∴∠FMC=∠DAC,∠GNC=∠EBC,四边形MHNC是平行四边形
∴∠HMC=∠HNC
又∵AD=AC,BC=BE, ∠ACD=∠BCE,
∴FM=HN,MH=GN,∠DAC=∠EBC
∴∠ =∠HNG
∴△FMH≌△HNG
∴FH=GH
(2)证法一:如图1,∵AD=AC,CB=CE,∠ACD=∠BCE,
∴∠DAC=∠CBE
∵∠FHG=180°-∠AHF-∠BHG=180°-(180°-2∠FAH)-(180°-2∠HBG)
=2∠FAH+2∠HBG-180°
=2(∠FAC+∠CAB)+2(∠CBG+∠CBA)-180°
=∠DAC+∠CBE+2(∠CAB+∠CBA)-180°
=2∠DAC+2(180°-∠ACB)-180°
=2∠DAC+2∠ACD-180°
=∠DAC+∠DAC+2∠ACD-180°=∠DAC,
∴∠FHG=∠DAC
证法二:如图2,∵△FMH≌△HNG,
∴∠MHF=∠NGH,∠MFH=∠NHG
又∵四边形MHNC为平行四边形,
∴∠FHG=∠MHN-(∠MHF+∠NHG)
=∠MHN-(180°-∠FMH)
=∠MHN+∠FMH-180°
=∠ACN+∠FMH-180°
=180°+∠FMC-180°
=∠FMC=∠DAC
∴∠FHG=∠DAC


科目:初中数学 来源:江苏中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第24章《图形的相似》中考题集(30):24.4 中位线(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com