
����Ŀ����֪�����������ֱ�����300ǧ��A��B����ͬʱ����������У����м���B�غ��������أ���ͼ����������Գ����صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ�� 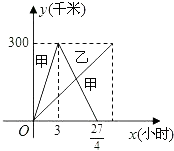
��1����׳�������صľ���y����ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2�����dz��� ![]() Сʱʱ������Գ����صľ�����ȣ����ҳ�������صľ���y����ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
Сʱʱ������Գ����صľ�����ȣ����ҳ�������صľ���y����ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
���𰸡�
��1���⣺��0��x��3ʱ������������������Ϊy=kx��
x=3ʱ��y=300��������k=100������y=100x��
��3��x�� ![]() ʱ����һ�κ�������Ϊy=kx+b��
ʱ����һ�κ�������Ϊy=kx+b��
�������㣨3��300������ ![]() ��0������
��0������ 
��� ![]() ��
��
����y=540��80x��
�ۺ����ϵü׳�������صľ���y����ʻʱ��x֮��ĺ�����ϵʽ Ϊ��y= 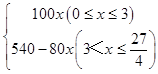 ��
��
��2���⣺��x= ![]() ʱ��y��=540��80��
ʱ��y��=540��80�� ![]() =180��
=180��
�ҳ����㣨 ![]() ��180����y��=40x����0��x��
��180����y��=40x����0��x�� ![]() ��
��
��3���⣺������������������
�ٵ�0��x��3��100x+40x=300�����x= ![]() ��
��
�ڵ�3��x�� ![]() ʱ����540��80x��+40x=300�����x=6��
ʱ����540��80x��+40x=300�����x=6��
����������������һ������ʱ��Ϊ�� ![]() Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��
Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��
����������1����ͼ֪���ú�����ϵ�ڲ�ͬ��ʱ������ֳɲ�ͬ�Ĺ�ϵ����ֶα������ʻʱ��С��3ʱ������������������ʹʱ�����3СʱС�� ![]() Сʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ����2��4.5Сʱ����3Сʱ������һ�κ�����ϵʽ��������ҳ�������
Сʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ����2��4.5Сʱ����3Сʱ������һ�κ�����ϵʽ��������ҳ������� ![]() Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮��3������������У�����ʱ�ס���������ʹ�ľ���֮��Ϊ300ǧ�ף��г����̽��������������������
Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮��3������������У�����ʱ�ס���������ʹ�ľ���֮��Ϊ300ǧ�ף��г����̽��������������������


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2��4x��4�ϵ�һ�����ǣ� ��
A.��4��4��B.��3����1��C.����2����8��D.����1��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��� A��������(-1,2) .����A����x ��ĶԳƵ㣬�õ���A1 ���ٽ���A1 ����ƽ�� 4����λ���õ���A2 �����A2 ��������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() ����
����![]() ������
������![]() ��
��![]() ������ֱ���
������ֱ���![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ���˶����Ե�
���˶����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��
��Ϊ�뾶��![]() ����
����![]() �˶�����
�˶�����![]() ���ı���
���ı���![]() ��������ʱ��
��������ʱ��![]() ��������Ϊ .
��������Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�������ȶ��Ե��ǣ�������
A. ƽ���ı��� B. ֱ�������� C. ������ D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�2����3��������A����x��ĶԳƵ㣬�õ���A�䣬������A�����y��ĶԳƵ㣬�õ���A�壬���A��������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε����߳��ֱ�Ϊ13cm��6cm����ô�����߳�Ϊ�� ��
A.7cmB.13cmC.6cmD.8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������3xy=27x3y4 �� ������Ӧ��ĵ���ʽ�ǣ� ��
A.3x3y4B.9x2y2C.3x2y3D.9x2y3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com