
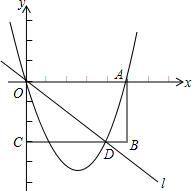
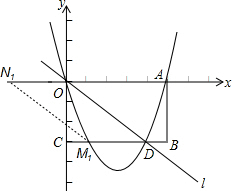
 已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线y=-
已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线y=-| 3 |
| 4 |
| 3 |
| 4 |
|
|
| 3 |
| 4 |
| 15 |
| 4 |
| 32+42 |
| 3 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
5-
| ||
| 2 |
5+
| ||
| 2 |
5-
| ||
| 2 |
5+
| ||
| 2 |
5-
| ||
| 2 |
5+
| ||
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、商家卖鞋,最关心的是鞋码的中位数 |
| B、数据2,5,7,x,3,3,6的平均数为4,则这组数据的极差是5 |
| C、要了解全市人民的低碳生活状况,适宜采用普查的方法 |
| D、随机抽查甲、乙两名同学的5次数学成绩,计算的平均分都是90分,方差分别为s甲2=5,s乙2=12,说明乙的成绩较为稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
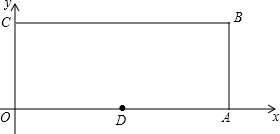 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 在?ABCD中,F是AD的中点,延长BC到点E,使CE=
在?ABCD中,F是AD的中点,延长BC到点E,使CE=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.
将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com