
分析 (1)首先化简二次根式,然后合并同类二次根式即可;
(2)首先化简二次根式,然后根据乘法交换律和结合律计算即可;
(3)根据平方差公式计算即可;
(4)首先化简二次根式,然后从左向右依次计算即可.
解答 解:(1)$\sqrt{50}$-($\sqrt{8}$+$\frac{2}{5}$$\sqrt{\frac{1}{2}}$)+$\sqrt{(\sqrt{2}-3)^{2}}$
=5$\sqrt{2}$-(2$\sqrt{2}$+$\frac{\sqrt{2}}{5}$)+3-$\sqrt{2}$
=5$\sqrt{2}$-2$\sqrt{2}$-$\frac{\sqrt{2}}{5}$-$\sqrt{2}$+3
=$\frac{9}{5}\sqrt{2}$+3
(2)$\sqrt{2\frac{1}{4}}$÷3$\sqrt{28}$×(-5)$\sqrt{2\frac{2}{7}}$
=$\frac{3}{2}$$÷6\sqrt{7}$×(-20)×$\frac{\sqrt{7}}{7}$
=[$\frac{3}{2}×(-20)$]×[$\frac{\sqrt{7}}{7}÷6\sqrt{7}$]
=(-30)×$\frac{1}{42}$
=-$\frac{5}{7}$
(3)($\sqrt{5}$+$\sqrt{2}$)2-($\sqrt{5}$-$\sqrt{2}$)2
=[($\sqrt{5}$+$\sqrt{2}$)+($\sqrt{5}$-$\sqrt{2}$)]×[($\sqrt{5}$+$\sqrt{2}$)-($\sqrt{5}$-$\sqrt{2}$)]
=2$\sqrt{5}$×$2\sqrt{2}$
=4$\sqrt{10}$
(4)$\frac{2}{3}$$\sqrt{27{a}^{3}}$-a2$\sqrt{\frac{3}{a}}$+6a$\sqrt{\frac{a}{3}}$-$\frac{a}{2}$$\sqrt{108a}$
=$\frac{2}{3}×3a\sqrt{3a}$-a2×$\frac{\sqrt{3a}}{a}$+6a×$\frac{\sqrt{3a}}{3}$$-\frac{a}{2}$×$6\sqrt{3a}$
=2a$\sqrt{3a}$$-a\sqrt{3a}$$+2a\sqrt{3a}$-3a$\sqrt{3a}$
=a$\sqrt{3a}+2a\sqrt{3a}-3a\sqrt{3a}$
=0
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是(2,-1).
如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是(2,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
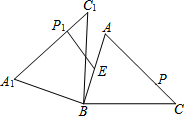 如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1B1C1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,线段EP1长度的最小值是$\frac{5\sqrt{2}}{2}$-2.
如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1B1C1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,线段EP1长度的最小值是$\frac{5\sqrt{2}}{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com