
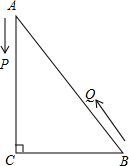
 在Rt△ABC中,AC=8,BC=6,一个运动的点P 从点A出发,以每秒钟1个单位的速度向点C运动,同时一个运动的点Q从点B出发,以每秒钟2个单位的速度向点A运动,当一个点到达终点时另一个点也随之停止.运动的时间为t秒.
在Rt△ABC中,AC=8,BC=6,一个运动的点P 从点A出发,以每秒钟1个单位的速度向点C运动,同时一个运动的点Q从点B出发,以每秒钟2个单位的速度向点A运动,当一个点到达终点时另一个点也随之停止.运动的时间为t秒. ;
; >5,则不存在这样的时间t.
>5,则不存在这样的时间t.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com