

 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×130°=65°,
×130°=65°, ∠A+90.
∠A+90. ∠ABC+
∠ABC+ ∠ACB=180°,
∠ACB=180°, ∠A+90°;
∠A+90°; ∠DBC=
∠DBC= ∠A+
∠A+ ∠ACB,
∠ACB, ∠BCE=
∠BCE= ∠A+
∠A+ ∠ABC,
∠ABC, (∠ACB+∠ABC)=90°-
(∠ACB+∠ABC)=90°- ∠A,
∠A, ∠DBC+
∠DBC+ ∠BCE=
∠BCE= ∠A+
∠A+ ∠ACB+
∠ACB+ ∠A+
∠A+ ∠ABC,
∠ABC, ∠ACB+
∠ACB+ ∠ABC,
∠ABC, ∠A,
∠A, ∠A;
∠A; ∠A.
∠A. ∠A.
∠A. ∠DBC=
∠DBC= ∠A+
∠A+ ∠ACB,同理可得:
∠ACB,同理可得: ∠BCE=
∠BCE= ∠A+
∠A+ ∠ABC,再利用三角形内角和定理以及外角和定理求出即可;
∠ABC,再利用三角形内角和定理以及外角和定理求出即可;

科目:初中数学 来源: 题型:
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:查看答案和解析>>
科目:初中数学 来源: 题型:
 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )查看答案和解析>>
科目:初中数学 来源: 题型:
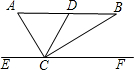 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com