
 ,确定m的值.
,确定m的值.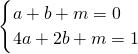 ,
,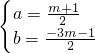 ,
, x2-
x2- x+m;
x+m; x2-
x2- x+m=0有两个不相等的实数根,
x+m=0有两个不相等的实数根, )2-4×
)2-4× m>0,
m>0, ≠0,
≠0, x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2).
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2). x2-
x2- x+m=-x+1,
x+m=-x+1,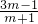 ,x1•x2=
,x1•x2=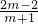 ;
;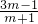 )2-4×
)2-4×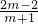 =(
=(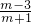 )2;
)2;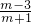 )2;
)2; ,
, )2,
)2,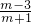 )2=8,
)2=8,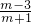 =±2,
=±2, .
. .
. x2-
x2- x+m;
x+m; x2-
x2- x+m的图象与x轴有两个交点,所以一元二次方程
x+m的图象与x轴有两个交点,所以一元二次方程 x2-
x2- x+m=0的判别式△>0且
x+m=0的判别式△>0且 ≠0,由此可求出m的取值范围;
≠0,由此可求出m的取值范围; x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(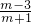 )2,再根据线段MN的长为2
)2,再根据线段MN的长为2 ,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.
,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.

科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com