
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
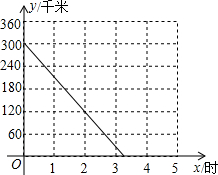 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab>0 | B. | a-b>0 | C. | a+b>0 | D. | a2+b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
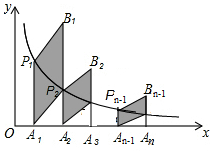 如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)
如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
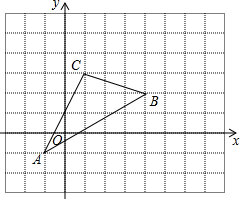 如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).
如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
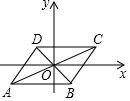 如图,已知?ABCD的顶点A在第三象限,顶点B在第四象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为(-a-2,-b).
如图,已知?ABCD的顶点A在第三象限,顶点B在第四象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为(-a-2,-b).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com