
 涪陵榨菜是重庆市农村经济中产销规模最大、品牌知名度最高、辐射带动能力最强的特色支柱产业.某知名榨菜企业为顺应市场需求推出了“五味榨菜”礼盒,成本为20元/盒.年销售量y(万盒)与售价x(元/盒)之间满足一次函数关系,其图象如图所示.
涪陵榨菜是重庆市农村经济中产销规模最大、品牌知名度最高、辐射带动能力最强的特色支柱产业.某知名榨菜企业为顺应市场需求推出了“五味榨菜”礼盒,成本为20元/盒.年销售量y(万盒)与售价x(元/盒)之间满足一次函数关系,其图象如图所示. ;③受公司生产规模及资金限制,公司的年产量不超过28万盒,广告投入不超过32万元.问公司在广告上投入多少资金可以使公司获得最大利润,最大利润为多少万元?(利润=总销售额-总成本-广告费)
;③受公司生产规模及资金限制,公司的年产量不超过28万盒,广告投入不超过32万元.问公司在广告上投入多少资金可以使公司获得最大利润,最大利润为多少万元?(利润=总销售额-总成本-广告费)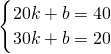 ,
,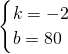 ,
,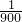 (a-30)2+2]-a
(a-30)2+2]-a a2+5a+200
a2+5a+200 (a-25)2+262.5,
(a-25)2+262.5,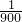 (a-30)2+2]≤28,
(a-30)2+2]≤28,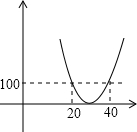
 (a-25)2+262.5中,当a<25时,w随a的增大而增大,
(a-25)2+262.5中,当a<25时,w随a的增大而增大, (20-25)2+262.5=260.
(20-25)2+262.5=260.

 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
 涪陵榨菜是重庆市农村经济中产销规模最大、品牌知名度最高、辐射带动能力最强的特色支柱产业.某知名榨菜企业为顺应市场需求推出了“五味榨菜”礼盒,成本为20元/盒.年销售量y(万盒)与售价x(元/盒)之间满足一次函数关系,其图象如图所示.
涪陵榨菜是重庆市农村经济中产销规模最大、品牌知名度最高、辐射带动能力最强的特色支柱产业.某知名榨菜企业为顺应市场需求推出了“五味榨菜”礼盒,成本为20元/盒.年销售量y(万盒)与售价x(元/盒)之间满足一次函数关系,其图象如图所示.| 1 | 900 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com