
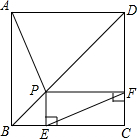
 已知点P是正方形ABCD的对角线BD上任一点,PE⊥BC于E,PF⊥CD于F,连PA、EF.猜想并证明线段PA与EF存在着什么关系.
已知点P是正方形ABCD的对角线BD上任一点,PE⊥BC于E,PF⊥CD于F,连PA、EF.猜想并证明线段PA与EF存在着什么关系. 解:猜想:线段PA与EF相等且互相垂直.
解:猜想:线段PA与EF相等且互相垂直.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
 如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.
如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.| A、> | B、= | C、< | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•海陵区模拟)已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.
(2013•海陵区模拟)已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:
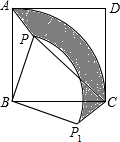 如图,已知点P是正方形ABCD内一点,连接PA、PB.将△PAB绕点B沿顺时针方向旋转90°到△P1CB的位置.设AB的长为3,PB的长为2,则△PAB旋转到△P1CB的位置的过程中,边PA所扫过的区域(图中阴影部分)的面积为
如图,已知点P是正方形ABCD内一点,连接PA、PB.将△PAB绕点B沿顺时针方向旋转90°到△P1CB的位置.设AB的长为3,PB的长为2,则△PAB旋转到△P1CB的位置的过程中,边PA所扫过的区域(图中阴影部分)的面积为| 5π |
| 4 |
| 5π |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.
已知点E是正方形ABCD中的CD的中点,F是边AD上一点,连接FE并延长交BC延长线于点G,AB=6.查看答案和解析>>
科目:初中数学 来源:2009-2010学年四川省南充市营山县九年级(上)期末数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com