
| A. | $\sqrt{a-2}$ | B. | $\sqrt{2-a}$ | C. | -$\sqrt{a-2}$ | D. | -$\sqrt{2-a}$ |
科目:初中数学 来源: 题型:解答题
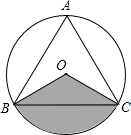 如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
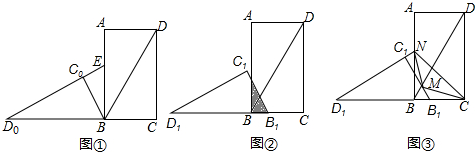
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
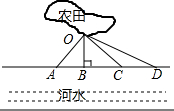 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )
春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )| A. | OA | B. | OB | C. | OC | D. | OD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com