
 ��tan��DOB=
��tan��DOB=
 �����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
�����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
 ��֪Rt��OHB����ֱ�DZߵıȣ�����ΪOB=10�����Կɸ��ݹ��ɶ��������B�����꣬�����������ʽ��
��֪Rt��OHB����ֱ�DZߵıȣ�����ΪOB=10�����Կɸ��ݹ��ɶ��������B�����꣬�����������ʽ��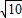 ��tan��DOB=
��tan��DOB= �������ù��ɶ������B�����ꣻ
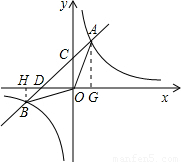
�������ù��ɶ������B�����ꣻ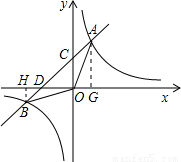 �⣺��1������A��AG��x���ڵ�G������B��BH��x���ڵ�H����Rt��OHB�У�
�⣺��1������A��AG��x���ڵ�G������B��BH��x���ڵ�H����Rt��OHB�У�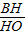 =
= ��
��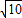 ��
��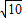 ��2��
��2��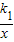 ��k1��0����
��k1��0����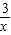 ��
��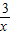 ��ͼ���ϣ�����õ�A��������Ϊ��m��
��ͼ���ϣ�����õ�A��������Ϊ��m��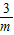 ����
���� ��OB=
��OB=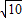 ��
��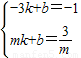 ��
��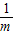 ��b=
��b=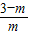 ��
��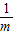 x+
x+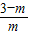 ��
��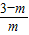 ����
����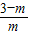 ��m+3��×
��m+3��× =
=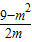 ��
��
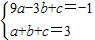 ��
��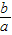 ��2-4•
��2-4•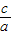 =9����c=2-3a��b=2a+1���룬
=9����c=2-3a��b=2a+1���룬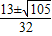 ��
��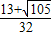 ʱ��b=2a+1=
ʱ��b=2a+1=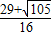 ��c=
��c=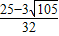 ��
��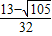 ʱ��b=
ʱ��b=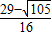 ��c=
��c=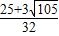
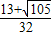 x2+
x2+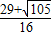 x+
x+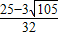 ��y=
��y=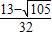 x2+
x2+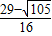 x+
x+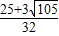 ��
��

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2010���㽭ʡ��������ɽ���п���ѧģ���Ծ�38�����ͳ��� ������ �ܹ⻪���������棩 ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2002�걱���ж������п���ѧ�Ծ��������棩 ���ͣ������
 ��tan��DOB=
��tan��DOB=
 �����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
�����жϹ�A��B�������������x���Ͻصõ��߶γ��ܷ����3������ܣ����ʱ�����ߵĽ���ʽ��������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2002�걱���ж������п���ѧ�Ծ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2002��ȫ���п���ѧ�����ࡶ���ݷ�������02���������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com