练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．方程x2-2x-6=0的两根为x1、x2，则|x1-x2|=2$\sqrt{7}$．

    分析 由方程x2-2x-6=0的两根为x1、x2，根据一元二次方程根与系数的关系，即可求得x1+x2=3，x1+x2=-1，又由代入求解即可求得答案．

    解答 解：∵方程x2-2x-6=0的两根为x1、x2，
    ∴x1+x2=2，x1+x2=-6，
    ∴|x1-x2|=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{2}^{2}-4×（-6）}$=2$\sqrt{7}$，
    故答案为：2$\sqrt{7}$．

    点评 此题考查了一元二次方程根与系数的关系以及分式的加减运算．此题难度不大，解题的关键是掌握：若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q性质的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．将两个完全相同的等腰直角三角形摆成如图的样子，假设图形中的所有点、线都在同一个平面内，两个三角形的重叠部分为△ADE，则图中有与△ADE相似的三角形吗？请找出来，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

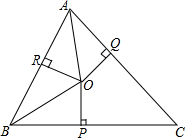    4．如图，已知在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR⊥AB于R，AB=7，BC=8，AC=9．
    （1）求证：OP=OQ=OR．
    （2）求BP、CQ、AR的长．
    （3）若BO的延长线交AC于E，CO的延长线交AB于F，若∠A=60゜，求证：OE=OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．有一弓行石桥，桥下的水面宽为2$\sqrt{21}$米，水面离弓顶的高度为3米，
    （1）求弓形所在圆的半径．
    （2）船一般的棚顶宽为4米，棚顶离水面的高度是2米，当水位上涨0.5米时，此船能通过吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：13=1=$\frac{1}{4}$×12×22；13+23=9=$\frac{1}{4}$×22×32；13+23+33=36=$\frac{1}{4}$×32×42；13+23+33+43=100=$\frac{1}{4}$×42×52；…
    （1）请你猜想填空：13+23+33+…+（n-1）3+n3=$\frac{1}{4}{n}^{2}（n+1）^{2}$；
    （2）试计算：13+23+33+…+993+1003．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）$\root{3}{8}$=2，$\root{3}{-8}$=-2；
    （2）$\root{3}{64}$=4，$\root{3}{-64}$=-4；
    （3）$\root{3}{125}$=5，$\root{3}{-125}$=-5；
     你发现了什么规律？用什么式子表示？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．现有四个有理数3，4，-6，10，请你用两种不同的算法计算出24，请分别写出三个算式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

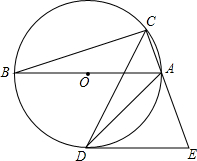    13．如图，⊙O是△ABC的外接圆，AB为⊙O的直径，∠ACB的平分线交⊙O于点D，点E在CA的延长线上，且DE为⊙O切线．
    （1）求证：AB∥DE；
    （2）连接AD，若tan∠ADC=$\frac{1}{3}$，AC=4，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：4（x+3y）2-（2x+3y）（2x-3y）

    查看答案和解析>>

    同步练习册答案