
如图14,已知CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.
(1)求证:AB是⊙O的切线;
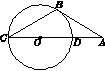
图14
(2)若⊙O的半径为2,求⌒BD的长.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
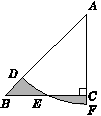
如图9,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为________(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
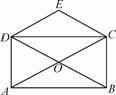
如图,矩形ABCD的对角线AC、BD、相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是( )
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
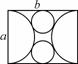
如图,用邻边长分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系是( )
A. b=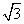 a B.b=
a B.b=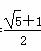 a C.b=
a C.b=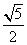 a D. b=
a D. b= a
a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com