
【题目】水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼.有关成本、销售额见右表:

(1)2012年,王大爷养殖甲鱼20亩,桂鱼10亩.求王大爷这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2012年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求王大爷原定的运输车辆每次可装载饲料多少kg?
【答案】(1)17万元;(2)甲鱼25亩,桂鱼5亩;(3)4000kg
【解析】
试题分析:(1)仔细分析题中数据特征即可列算式求解;
(2)先设养殖甲鱼x亩,则养殖桂鱼(30-x)亩,列不等式,求出x的取值,再表示出王大爷可获得收益为y万元函数关系式求最大值;
(3)设大爷原定的运输车辆每次可装载饲料a㎏,结合(2)列分式方程求解.
(1)2012年王大爷的收益为:![]() ;
;
(2)设养殖甲鱼x亩,则养殖桂鱼(30-x)亩.
由题意得![]() 解得
解得![]() ,
,
又设王大爷可获得收益为y万元,则![]() ,即
,即![]() .
.
∵函数值y随x的增大而增大,∴当x=25,可获得最大收益
答:要获得最大收益,应养殖甲鱼25亩,养殖桂鱼5亩;
(3)设王大爷原定的运输车辆每次可装载饲料akg,由(2)得,共需饲料为![]() ,根据题意,得
,根据题意,得![]() ,解得
,解得![]() .
.
答:王大爷原定的运输车辆每次可装载饲料4000kg.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABE≌△ACD,且AB=AC.
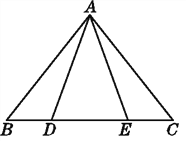
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C= ![]() ,其中正确的有( )
,其中正确的有( ) 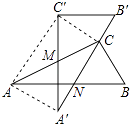
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.
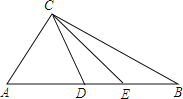
(1)若△CDE的周长为4,求AB的长;
(2)若∠ACB=100°,求∠DCE的度数;
(3)若∠ACB=a(90°<a<180°),则∠DCE=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com