
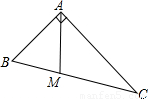
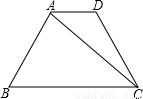
 (2009•上海)如图,在Rt△ABC中,∠BAC=90°,AB=3,M为BC上的点,连接AM,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,求点M到AC的距离.
(2009•上海)如图,在Rt△ABC中,∠BAC=90°,AB=3,M为BC上的点,连接AM,如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,求点M到AC的距离.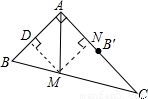 解:∵△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,假设这个点是B′,
解:∵△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,假设这个点是B′, ×3×6
×3×6 ×MD×3+
×MD×3+ ×6×MN,
×6×MN,

科目:初中数学 来源:2009年全国中考数学试题汇编《三角形》(18)(解析版) 题型:解答题
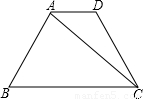
查看答案和解析>>
科目:初中数学 来源:2010年中考数学三轮复习每天30分综合训练(01)(解析版) 题型:选择题
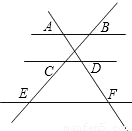
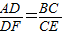

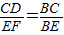
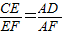
查看答案和解析>>
科目:初中数学 来源:2010年广东省中山市广外附设外语学校中考数学二模试卷(解析版) 题型:解答题
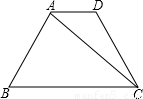
查看答案和解析>>
科目:初中数学 来源:2009年上海市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com