练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用反证法证明命题“三角形中最多有一个角是直角”时，下列假设正确的是（　　）

    A.三角形中最少有一个角是直角

    B.三角形中没有一个角是直角

    C.三角形中三个角全是直角

    D.三角形中有两个或三个角是直角

    【答案】D

    【解析】

    在反证法的步骤中，第一步是假设结论不成立，可据此进行解答．

    根据反证法的步骤，则可假设为三角形中有两个或三个角是直角．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一列单项式：﹣x2 ， 3x3 ， ﹣5x4 ， 7x5 ， …，按此规律排列，则第7个单项式为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一次函数y＝(m－3)x＋5的函数值y随x的增大而增大，则(　　)

    A. m＞0 B. m＜0 C. m＞3 D. m＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于多项式a3b﹣a2+ab﹣1，下列叙述正确的是（　　）

    A. 它是四次四项式B. 它是三次四项式

    C. 它是四次三项式D. 它是三次三项式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于圆的周长公式C=2πR，下列说法正确的是（ ）

    A. π、R是变量，2是常量 B. R是变量，π是常量

    C. C是变量，π、R是常量 D. C、R是变量，2、π是常量

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解
    如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
    探究发现
    （1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？（填“是”或“不是”）．
    （2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
    应用提升
    （3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
    请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】|a|的含义是：数轴上表示数a的点与原点的距离．则|﹣2|的含义是；若|x|=2，则x的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图．请根据相关信息，解答下列问题：

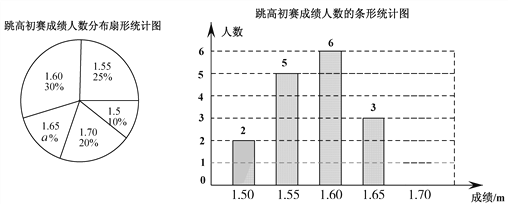
    （1）扇形统计图中，初赛成绩为1.65m所在扇形图形的圆心角为_ _°；

    （2）补全条形统计图；

    （3）这组初赛成绩的中位数是 m；

    （4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（ ）

    A.16
    B.12
    C.8
    D.4

    查看答案和解析>>

    同步练习册答案