解:(1)AE=CG,AE⊥CG.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∵在△ADE和△CDG中,
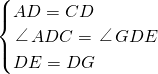
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,
∵∠CGD+∠DCG=90°,
∴∠AED+∠DCG=90°,
∴∠EMC=180°-(∠AED+∠DCG)=180°-90°=90°,
∴AE⊥CG;
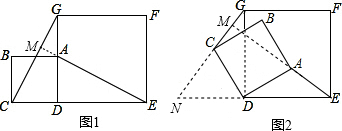
(2)结论还成立.
理由如下:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠GDE=90°,
∴∠ADC-∠ADG=∠GDE-∠ADG,
即∠ADE=∠CDG,
∵在△ADE和△CDG中,
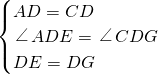
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠CGD=∠AED,
延长AE交CG于M,延长GC交ED的延长线于N,
∵∠CGD+∠N=90°,
∴∠AED+∠N=90°,
∴∠EMN=180°-(∠AED+∠N)=180°-90°=90°,
∴AE⊥CG.
分析:(1)根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠GDE=90°,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应边相等可得AE=CG,全等三角形对应角相等可得∠CGD=∠AED,延长AE交CG于M,根据∠CGD+∠DCG=90°求出∠AED+∠DCG=90°,然后求出∠CME=90°,再根据垂直的定义即可得解;
(2)根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠GDE=90°,然后求出∠ADE=∠CDG,然后利用“边角边”证明△ADE和△CDG全等,根据全等三角形对应边相等可得AE=CG,全等三角形对应角相等可得∠CGD=∠AED,延长AE交CG于M,延长GC交ED的延长线于N,根据∠CGD+∠N=90°求出∠AED+∠N=90°,然后求出∠CME=90°,再根据垂直的定义即可得解.
点评:本题考查了正方形的性质,全等三角形的判定与性质,以及垂直的定义,熟记正方形的性质确定出三角形全等的条件是解题的关键.

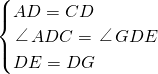 ,
,
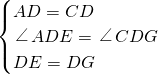 ,
,

 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )