

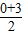 ����x=
����x= ��
�� ���������ߵĽ���ʽΪ����ʽy=a��x-
���������ߵĽ���ʽΪ����ʽy=a��x- ��2+k����B������Ϊ��
��2+k����B������Ϊ�� ��k�����ٽ�x=
��k�����ٽ�x= ���룬�����C��������Ϊ9a+k������MC=4.5�����a=
���룬�����C��������Ϊ9a+k������MC=4.5�����a= ��Ȼ��A�����꣨3��0������y=
��Ȼ��A�����꣨3��0������y= ��x-
��x- ��2+k�����k=-
��2+k�����k=- ���õ������ߵĽ���ʽΪy=
���õ������ߵĽ���ʽΪy= ��x-
��x- ��2-
��2- ����y=
����y= x2-
x2- x��
x�� ���룬���y��ֵ�����ɵõ�D�����ꣻ
���룬���y��ֵ�����ɵõ�D�����ꣻ a2������������֮��ľ��빫ʽ���EF=3
a2������������֮��ľ��빫ʽ���EF=3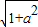 ����
����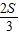 =
=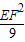 -1��������ó�S=
-1��������ó�S= EF2-
EF2- ����S��EF���ȵĶ��κ�����
����S��EF���ȵĶ��κ����� ��
�� ��
�� ��2+k��
��2+k�� ��k����
��k���� +3=
+3= ����C��������y=a��x-
����C��������y=a��x- ��2+k�ϣ�
��2+k�ϣ� -
- ��2+k=9a+k��
��2+k=9a+k��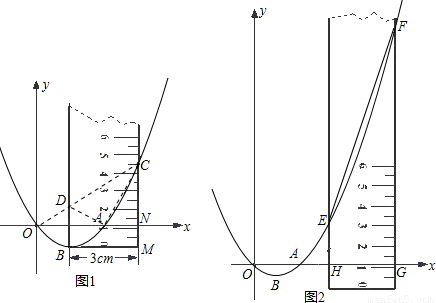 ��MC=4.5��
��MC=4.5�� ��
�� ��x-
��x- ��2+k��
��2+k�� ��3-
��3- ��2+k=0�����k=-
��2+k=0�����k=- ��
�� ��x-
��x- ��2-
��2- ����y=
����y= x2-
x2- x��
x�� ��
��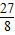 �����룬
�����룬 m=
m=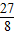 �����m=
�����m= ��
�� x��
x�� ʱ��y=
ʱ��y= ×
× =
= ��
�� ��
�� ����
���� a2-
a2- a����H��������a��0����
a����H��������a��0���� ��a+3��2-
��a+3��2- ��a+3������G��������a+3��0����
��a+3������G������Ϊ��a+3��0���� ��EH+FG��•HG=
��EH+FG��•HG= [��
[�� a2-
a2- a��+
a��+ ��a+3��2-
��a+3��2- ��a+3��]×3=
��a+3��]×3= a2��
a2�� ��a+3��2-
��a+3��2- ��a+3��-��
��a+3��-�� a2-
a2- a��=3a��EF=
a��=3a��EF=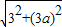 =3
=3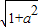 ��
��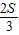 =
=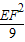 -1��
-1�� EF2-
EF2- ����S��EF���ȵĶ��κ�����
����S��EF���ȵĶ��κ�����

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��
18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com