
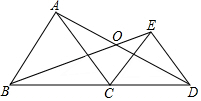
 如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是①②.
如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是①②. 分析 证明△BCE≌△ACD(SAS),即可判断.
解答 解:∵△ABC和△ECD都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=∠BAC=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,
∵∠BCE=∠ACD,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴BE=AD,故①正确.
∵∠AOB=∠EBC+∠ADC,
∴∠AOB=∠EBC+∠BEC=∠DCE=60°.
∵∠AOB+∠BOD=180°,
∴∠BOD=120°,故②正确,
不能证明OA=OD,③错误,
故选:①②.
点评 本题考查了等边三角形的性质的运用,三角形的外角与内角的关系的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是解答的关键.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
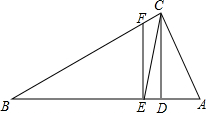 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不可能事件发生的概率为0 | |
| B. | 随机事件发生的概率为0 | |
| C. | 概率很小的事件不可能发生 | |
| D. | 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
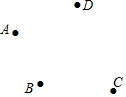 如图所示,平面上有四个点A、B、C、D,用直尺和圆规按要求作图:
如图所示,平面上有四个点A、B、C、D,用直尺和圆规按要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
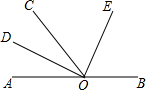 如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com