
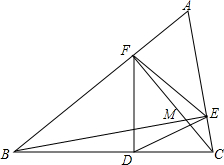
 如图,△ABC,∠A=60°,BE⊥AC于点F,点D是BC中点,BE与CF相交于M
如图,△ABC,∠A=60°,BE⊥AC于点F,点D是BC中点,BE与CF相交于M分析 (1)先根据直角三角形两锐角互余的性质求出∠ABE=∠ACF=30°,再根据三角形的内角和定理求出∠BCF+∠CBE=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BDF+∠CDE=120°,从而得到∠EDF=60°,再根据直角三角形斜边上的中线等于斜边的一半可得DE=DF,根据有一个角是60°的等腰三角形是等边三角形即可证明;
(2)根据30°角所对的直角边等于斜边的一半可得BM=2FM,ME=$\frac{1}{2}$CM,然后代入数据进行计算即可求解.
解答 (1)证明:∵∠A=60°,BE⊥AC,CF⊥AB,
∴∠ABE=∠ACF=90°-60°=30°,
在△ABC中,∠BCF+∠CBE=180°-60°-30°×2=60°,
∵点D是BC的中点,BE⊥AC,CF⊥AB,
∴DE=DF=BD=CD,
∴∠BDF=2∠BCF,∠CDE=2∠CBE,
∴∠BDF+∠CDE=2(∠BCF+∠CBE)=2×60°=120°,
∴∠EDF=60°,
∴△DEF是等边三角形;
(2)解:∵∠A=60°,BE⊥AC,CF⊥AB,
∴∠ABE=∠ACF=90°-60°=30°,
∴BM=2FM=2×4=8,ME=$\frac{1}{2}$CM=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴BE=BM+ME=8+$\frac{3}{2}$=$\frac{19}{2}$.
点评 本题主要考查了等边三角形的判定与性质,等腰三角形三线合一的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,仔细分析图形并熟练掌握性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
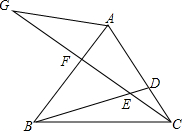 在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.
在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
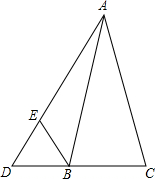 已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.
已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com