解:设该反比例函数的解析式为y=

(k≠0),则
2=
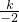
,
解得,k=-4;
所以,该反比例函数的解析式为y=-

;
∵-4<0,
∴该反比例函数经过第二、四象限,且在每一象限内,y随x的增大而增大;
(2)由(1)知,该反比例函数的解析式为y=-

,则xy=-4.
∵-2×4=-8≠-4,3×(-

)=-4,2

×(-

)=-4,
∴点B(4,-2)不在该函数图象上,点C(3,

)和D(
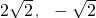
)在该函数图象上;
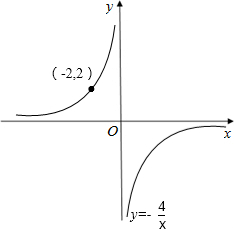
(3)反比例函数的图象过点A(-2,2),由(1)知,该反比例函数经过第二、四象限,且在每一象限内,y随x的增大而增大;所以其图象如图所示:
分析:(1)利用待定系数法求反比例函数的解析式;
(2)根据反比例函数图象上点的坐标特征,将B、C、D三点分别代入进行验证即可;
(3)根据该反比例函数所在的象限、以及该函数的单调性画出图象.
点评:本题考查了反比例函数的图象与性质、待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特征.经过函数的某点一定在该函数的图象上.

 已知反比例函数的图象过点A(-2,2).
已知反比例函数的图象过点A(-2,2). )和D(
)和D(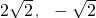 )哪些点在图象上?
)哪些点在图象上? (k≠0),则
(k≠0),则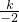 ,
, ;
; ,则xy=-4.
,则xy=-4. )=-4,2
)=-4,2 ×(-
×(- )=-4,
)=-4, )和D(
)和D(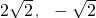 )在该函数图象上;
)在该函数图象上;

