
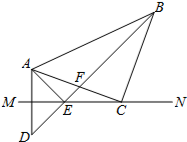
 如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.
如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE. 分析 (1)连接CD,利用轴对称的性质进行解答即可;
(2)根据勾股定理进行解答即可.
解答 解:(1)连接CD,
∵MN垂直平分AD,点C,E在MN上,
∴根据点A,D关于MN的对称性,得 CA=CD,∠MCD=∠MCA,∠CAE=∠CDE,
∵CA=CB,
∴CB=CD,
∴∠CBE=∠CDB,
∴∠CBE=∠CAE,
∵∠MCA=20°,
∴∠MCD=20°,
∵∠ACB=90°,
∴∠BCD=130°,
∴∠CBE=∠CDB=25°,
∠CAE=∠CDB=∠CBE=25°;
(2)∵∠CFE既是△AEF的外角又是△BCF的外角,
∴∠CFE=∠CAE+∠AEF=∠CBF+∠FCB,
∵∠CAE=∠CBE,
∴∠AEB=∠ACB=90°,
∴AE2+BE2=AB2,
∵∠ACB=90°,CA=CB,AC=5,
∴AB2=AC2+BC2=50,
∴AE2+BE2=AB2=AC2+BC2=50.
点评 本题考查的是轴对称的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | |
| A | B | |
| 创新 | 85 | 70 |
| 综合知识 | 50 | 80 |
| 语言 | 88 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
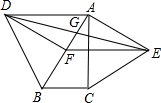 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方式1 | 方式2 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.20元/分钟 | 0.40元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | C | |
| a | 40 | 10 | 10 |
| b | 3 | 24 | 3 |
| c | 2 | 2 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com