
 如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$.
如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$. 分析 连接PA、PB、PC利用等面积的知识可求出PD+PE+PF的和的值.
解答  解:连接PA、PB、PC,
解:连接PA、PB、PC,
∵△ABC是边长为1的正三角形,
∴可得三角形ABC的面积为$\frac{\sqrt{3}}{4}$,
SABC=SAPB+SAPC+SBPC=$\frac{1}{2}$×1×PE+$\frac{1}{2}$×1×PF+$\frac{1}{2}$×1×PD=$\frac{1}{2}$(PD+PE+PF),
∴可得PD+PE+PF=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$
点评 本题考查了等边三角形的性质,难度不大,解决本题的关键是利用等面积法确定答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
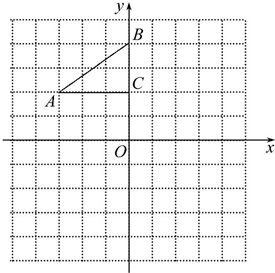 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 土特产品种 | 甲 | 乙 | 丙 |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨土特产获利(百元) | 12 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-2,-5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b-$\frac{m}{x}$>0的解集是-2<x<0或x>5.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(-2,-5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b-$\frac{m}{x}$>0的解集是-2<x<0或x>5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF=$\frac{2}{3}$EH,求EH的长.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF=$\frac{2}{3}$EH,求EH的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
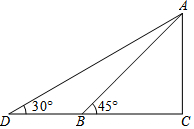 如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上.
如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平面直角坐标系中,直线AB与x轴交于点A(3,0),与反比例函数在第三象限内的图象交于点B(-1,a),连接BO,若S△AOB=3.
如图,已知平面直角坐标系中,直线AB与x轴交于点A(3,0),与反比例函数在第三象限内的图象交于点B(-1,a),连接BO,若S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
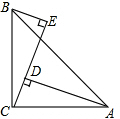 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CE于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com