

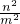 •S1,
•S1, •S1,
•S1, •S1-2•
•S1-2• •S1=S1(1+
•S1=S1(1+ -2•
-2• )=S1(1-
)=S1(1- )2,
)2, )2>0,
)2>0,

 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
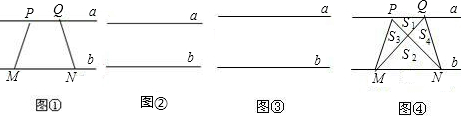
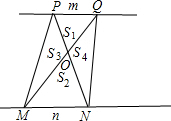 如图,若梯形PMNQ是一块绿化地,梯形上底PQ=m,下底MN=n,现在计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻,为了节省费用,园艺师应该把哪两块地种植较便宜的花草?通过计算说明你的理由.
如图,若梯形PMNQ是一块绿化地,梯形上底PQ=m,下底MN=n,现在计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻,为了节省费用,园艺师应该把哪两块地种植较便宜的花草?通过计算说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第29章《相似形》中考题集(28):29.8 相似三角形的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com